०२

CONSTRUCTION OF SQUARE, SURD, A SQUARE FROM A COMBINA- TION AND DIFFERENCE OF TWO SQUARES, AND TRANSFORMATION OF A RECTANGLE INTO A SQUARE

This chapter mainly deals with the methods of construction and transformation of geometrical figures like square and rectangle, already dealt by Baudhāyana.

अथापरोयोगः ॥ २.१ ॥

Now another method of construction (of a square).

अथापरोयोगः ॥ २.१ ॥

विहरणाविशेषः इत्यर्थः ॥

पृष्ठ्यान्तयोर्मध्ये च शङ्कून्निहत्यार्धेऽर्धे तद्विशेषमभ्यस्य लक्षणं कृत्वार्धमगमयेत् । अन्त्ययोः पाशौ कृत्वा मध्यमे सविशेषं प्रतिमुच्य पूर्वस्मिन्नितरं लक्षणेन दक्षिणमङ्कमायच्छेत् । उन्मुच्य पूर्वस्मादपरस्मिन् प्रतिमुच्य लक्षणेनैव दक्षिणां श्रोणिमायच्छेत् । एवमुत्तरौ श्रोण्यंसौ ॥ २.१ ॥

Poles are fixed at both ends and in the middle of the east-west line. A cord measuring half of the east-west line is taken and increased by its viśeșa (the difference between its length and the diagonal of the square produced by it). After giving a mark at this point, the cord is (further) increased by half of the east-west line. Ties are made at both ends of the cord. Fixing the tie at the saviśeșa end at the middle pole and the other tie at the eastern pole, the cord is stretched by the mark so as to obtain the south-eastern corner. By removing the tie from the eastern pole and fixing it to the western pole, the south-western corner is likewise obtained by (stretching the cord with) the mark. In the same way, the north-western and the north-eastern corners (are obtained).

2.1. Construction of a square. Apastamba des-cribes here an interesting method of construction of a square. In Fig. 2, EW represents the east-west line, 2a; XU the given cord, a; XV the saviśeșa of a, √2a; and VY the half cord, a.

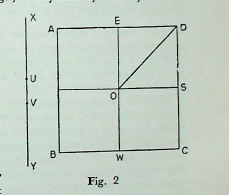
The cord XY is prepared for its use in the construction of the square.

The knots at X and Y are tied at ◊ and E respectively and the cord is stretched by the mark V, which gives the south-east corner D. Then the knot at E is taken off and fixed at W. The cord is likewise stretched by the mark V, which fixes the south-western corner C. The process is repeated in the north-eastern and the north-western side. ABCD is the required construction of the square.

पृष्ठ्यान्तयोर्मध्ये च शङ्कून्निहत्यार्धेऽर्धे तद्विशेषमभ्यस्य लक्षणं कृत्वार्धमगमयेत् । अन्त्ययोः पाशौ कृत्वा मध्यमे सविशेषं प्रतिमुच्य पूर्वस्मिन्नितरं लक्षणेन दक्षिणमङ्कमायच्छेत् । उन्मुच्य पूर्वस्मादपरस्मिन् प्रतिमुच्य लक्षणेनैव दक्षिणां श्रोणिमायच्छेत् । एवमुत्तरौ श्रोण्यंसौ ॥ २.१ ॥

चतुरश्रप्रमाणान्तयोःशङ्कुं निहत्य तयोर्मध्ये च शङ्कुं निहत्य अर्धेप्रमाणार्धे, तद्विशेषंतस्यार्धस्य विशेषं, प्रमाणं तृतीयेन वर्धयेदिति न्यायेन लक्षणं कृत्वा पुनरागमयेत्प्रक्षिपेत् । अन्त्ययोः पाशौ कृत्वा मध्यमे शङ्कौ सविशेषं पाशं प्रतिमुच्य पूर्वस्मिन् शङ्कौ इतरं पाशं प्रतिमुच्य लक्षणेन दक्षिणेनापसार्य शङ्कुं निहन्यात् । स दक्षिणांसः । पूर्वस्माच्छङ्कोः पाशमपरस्मिन् शङ्कौ प्रतिमुच्य तेनैव लक्षणेन दक्षिणं श्रोणिमायच्छेत् । तेनैवोदगपसार्य उत्तरां श्रोणिं विपर्यस्योत्तरमंसम् ॥

योगद्वयमिदं समचतुरश्रस्य सम्यक् ॥

करविन्दीया व्याख्या

(अथापरो श्रोण्यंसौ)

प्रमाणमात्रीं रज्जुमित्येव, विहरणोपायो योग इत्युक्तं, पृष्ठ्यान्तयोः मध्ये च शङ्कुं निहत्य । व्याख्यातमेतत् । अर्धेप्रमाणामात्रचा रज्ज्वा अर्धे तद्विशेषमभ्यस्य संयोज्य लक्षणं कृत्वा सूत्रसविशेषार्धान्ते अर्धं आगमयेत्शिष्टं यथा प्रमाणं भवति तथाऽगमयेत्, अयमर्थःर्धद्विकरणीमात्रीं केवलार्धमात्रीं च एकां रज्जुं मीत्वार्धद्विकरणी मात्रे लक्षणं कृत्वा रज्ज्वन्तौ पाशौ कृत्वा मध्यमे शङ्कौ सविशेषमर्धं प्रतिमुच्य पूर्वस्मिन् शङ्कौ केवलमर्धं प्रतिमुच्य लक्षणेन दक्षिणमंसमायच्छेत्कुर्यात् । उन्मुच्य पूर्वस्मादिति स्पष्टार्थः । अयमपि योगःसमचतुरश्रविषय एव । अर्धे तद्विशेषमिति प्रमामसविशेषयोः प्रस्तुतत्वात्प्रसङ्गेनोच्यते ।

सुन्दरराजीया

(अथापरो श्रोण्यंसौ)

अर्धेप्रमाणार्धमात्रे शुल्बे । तद्विशेषंर्धस्यैव विशेषं अभ्यस्य तद्विशेषान्ते लक्षणं कृत्वा अन्यदर्धं निर्विरोषमागमयेत् । यथागार्हपत्यचितेः षण्णवत्यङ्गुलाया अन्तययोर्मध्ये च शङ्कून्निहत्य अर्वेऽष्टाचत्वारिंशदङ्गुले तद्विरोषं चतुस्तिलोनं विंशत्यङ्गुलमभ्यस्य लक्षणं कृत्वान्यदर्धं अष्टाचत्वारिंशदङ्गुलं संयोजयेत् । एवं चतुस्तिलोनषोडशकोत्तरशताङ्गुलं शुल्बम् । अन्तयोरित्यादि स्पष्टम् ।

कपर्दिभाष्यम्

प्रमाणं तिर्यग्द्विकरण्यायामस्तस्याक्ष्णयारज्जुस्त्रिकरणी ॥ २.२ ॥

The breadth (of a rectangle) being the side of a given square (pramāṇa) and the length the side of a square twice as large (dvikaraṇī), the diagonal equals the side of a square thrice as large (tṛkaraṇī).

प्रमाणं तिर्यग्द्विकरण्यायामस्तस्याक्ष्णयारज्जुस्त्रिकरणी ॥ २.२ ॥

प्रमाणंप्रक्रमादेस्तिर्यङ्नानी । द्विकतणीपार्श्वमानीतस्यैव प्रक्रमादेः । तस्यैवंभूतस्य दीर्घचतुरश्रस्याक्ष्णयारज्जुस्त्रिकरणीत्रिगुणां भूमिं करोति । तस्य तिर्यङ्भानीभूदस्य । कथं ? प्रमाणमेकं करोति पार्श्वमानी द्विकरणी सा द्वौ करोति । तदुभयमक्ष्णयारज्जुः करोति । तदुक्तं दीर्घस्याक्ष्णयारज्जुः । इति

तृतीयकरण्येतेन व्याख्याता । विभागस्तु नवधा ॥ २.३ ॥

Thereby is explained the side of a square one-third the area of a given square (tṛtiyakaraņi). It is the side of a square one-ninth the area of the square (explained in the preceding rule, that is, of the square on the tṛkaraṇī).

2.2-2.3. Surd. Dvikaraņi means √2 a, where a is the measure; likewise tṛkaraņi is √3a, and tṛtiyakaraṇi = 1/√3 a. For details vide our discussion under Bśl. 1.9-1.11.

तृतीयकरण्येतेन व्याख्याता । विभागस्तु नवधा ॥ २.३ ॥

एतेनैव मार्गेण तृतीयकरणी व्याख्याता । अनयैव त्रिकरण्या तृतीयकरण्यप्यवगन्तुं शक्येत्यर्थः । कथमित्याहत्रिकरणीक्षेत्रं नवधा विभज्य एकं भागं गृह्णीयात् । प्रमाणतृतीयं भवति । त्रिकरण्याः तृतीयं करोति । तत्र श्लोकः

अक्ष्णारज्जुस्त्रिकृत्प्रोक्ता प्रमाणसविशेषयोः ।

अस्या एव तृतीयं तु तृतीयकरणीं विदुः ॥

करविन्दीया व्याख्या

(प्रमाणंत्रिकरणी)

प्रमाणद्विकरण्यक्ष्णयारज्जव उक्तः । यस्य चतुरश्रस्य प्रणाणं तिर्यङ्भानी द्विकरणी पार्श्वमानी तस्य चतुरश्रस्याक्ष्णयारज्जुः प्रमाणपार्श्वमानी तिर्यङ्भानी क्षेत्रस्य त्रिकरणीभवति ॥

तृतीयकरण्येतेन व्याख्याता ।

त्रिकरणीव्याख्याने तृतीयकरण्यपि व्याख्याता । कथं ? तृतीयं तिर्याग्द्विकण्यायामः, तस्याक्ष्णयारज्जुस्तृतीयकरणी ।

तृतीयकरण्यवगमायाह

(विभागस्तु नवधा) तृतीयकरण्यवगमे इयांस्तु विशेषः । क्षेत्रस्य नवधा विभागः कार्यः, कस्य क्षेत्रस्य ? प्रमाणक्षेत्रस्य त्रिकरणीक्षेत्रस्य वा । अयमर्थःयस्य क्षेत्रस्य तृतीयकरणी साध्यते तत्क्षेत्रं नवधा विभज्य तत्रकैस्य भागस्य पार्श्वमानीं तिर्यङ्भानीं कृत्वा तस्यैव भागस्याक्ष्णयारज्जुं पार्श्वमानीं कृत्वा ताभ्यां चतुरश्रे कृते चतुरश्रे नवधा विभक्ते तत्रैकस्य भागस्य करणीप्रमाणचतुरश्चक्षेत्रस्य तृतीयकरणी भवति । स च विभागः प्रमाणक्षेत्रतृतीयमिति प्रदर्शनम् । एतेन चतुष्करणीचतुर्थकरणीप्रभृतीनामपि । तथाहिप्रमाणं तिर्यक्चतुष्करण्यायामस्तस्याक्ष्णयारज्जुः पञ्चकरणी । तथा प्रमाणं तिर्यक्पञ्जकरण्यायामस्तस्याक्ष्मयारज्जुः षट्करणीत्याति द्रष्टव्यम् । तथाहिद्विकरणी तिर्यङ्भानी त्रिकरण्यायामः तस्याक्ष्णयारज्जुः पञ्चकरणी । तिर्यङ्भानी दशकरण्यायामस्तस्याक्ष्णयारज्जुः पञ्चदशकरणीत्याद्यपि द्रष्टव्यम् । तथा तुरीयं तिर्यक्त्रिकरण्यायामस्तस्याक्ष्णयारज्जुस्तुरीयकरणी । तथा पञ्जमं तिर्यक्चतुष्करण्यायामस्तस्याक्ष्णयारज्जुः पञ्चमकरणीत्यादि द्रष्टव्यम् । त्रिकरणीतृतीयकरण्योःसौत्रामण्यादावुपयागेः । ननु दीर्घस्याक्ष्णयारज्जुरित्यनेन त्रिकरणीतृतीयकरणीप्रभृतयः सिद्धाः । तत्किमर्थं त्रिकरण्यादिकरणीविधिरारभ्यते । उच्यतेद्विप्रकाराः करण्यः, शुद्धमूला अशुद्धमूलाश्च । शुद्धं मूलं यासां ताःशुद्धमूलाः । द्वाभ्यां चत्वारि, त्रिभिर्नवेत्यादिवक्ष्यमाणाश्वतुष्करणीनवकरणीप्रभृतयः तासां तु सर्वदा द्विकरणी त्रिकरणी पञ्चकरणीत्येव व्यपदेश इति प्रदर्शयितुमिदमुच्यते, द्वयोः करणी द्विकरणी, त्रयाणां करणी त्रिकरणी, चतुर्णां करणी चतुष्करणी, पञ्चानां करणी पञ्चकरणीति । किञ्च दीर्घस्याक्ष्णयारज्जुरित्यनेन सामान्येन नाञ्जसा त्रिकरणीप्रभृतीनामवगतिर्भवति । उक्तप्रकारेण संपन्नानां करणीनां तेन संवादमात्रं भवति । तद्युज्यत एव द्विकरण्यादिकरणीविशेषविध्यारम्भः ।

सुन्दरराजीया

अथ त्रिकरणीमाह

(प्रमाणंत्रिकरणी)

यथा द्वादशाङ्गुला तिर्यङ्भानी तद्द्विकरणी तिरोनसत्पदशाङ्गुला पार्श्वमानी । एवं दीर्घचतुरश्रे कृते तस्याक्ष्णयारज्जुर्विंशत्यङ्गुलयःसत्पविंशतितिलाश्च । सा त्रिकरणी प्रमाणपरिमितं क्षेत्रं त्रिगुणं करोति ॥

(तृतीयकरण्येतेन नवधा)

तृतीयकरण्या चतुरश्रे कृते नवधा विभागः कार्यः । तस्यैको भागः प्रमाणक्षेत्रस्य तृतीयं भवति । त्रिकरण्यास्तृतीयं तस्य करणी ॥

कपर्दिभाष्यम्

तुल्ययोश्चतुरश्रयोरुक्तः समासः । नानाप्रमाणयोश्चतुरश्रयोः समासः ॥ २.४ ॥

The combination of two equal squares has been described. The combination of two squares of unequal measures (sides) (now) follows.

तुल्ययोश्चतुरश्रयोरुक्तः समासः । नानाप्रमाणयोश्चतुरश्रयोः समासः ॥ २.४ ॥

समास एकीकरणम् । चतुरश्रस्याक्ष्णयारज्जुरिति सूत्रेणस्पष्टः । नानाप्रमाणयोश्चतुरश्रयोःसमास उच्यत इति शेषः । दीर्घस्य समस्य चतुरश्रस्य समास एकीकरणम् ।

ह्रसीयसः करण्या वर्षीयसो वृद्ध्रमुल्लिखेत् । वृद्ध्रस्याक्ष्णयारज्जुरुभे समस्यति । तदुक्तम् ॥ २.४ ॥

A (rectangular) part is cut off from the larger (square) with the side of the smaller; the diagonal of the cut-off (rectangular) part (produces the square which) combines both the squares. This has been stated.

ह्रसीयसः करण्या वर्षीयसो वृद्ध्रमुल्लिखेत् । वृद्ध्रस्याक्ष्णयारज्जुरुभे समस्यति । तदुक्तम् ॥ २.४ ॥

ह्रसीयसः अल्पीयसः क्षेत्रस्य करण्या प्रमाणेन वर्षीयसः वर्षीयसेत्यर्थः ।

वृद्ध्रं दीर्घमुल्लिखेत् । यथाल्पीयसः करणी तिर्यङ्भानी वर्षीयसः करणी पार्श्वमानी, तथा दीर्घचतुरश्रमुल्लिखेत् । वृद्ध्रस्याक्ष्णयारज्जुरुभे समस्यति । उक्तंदीर्घचतुरश्रस्याक्ष्णयारज्जुरिति ।

करविन्दीया व्याख्या

(तुल्ययोःसमासः)

तुल्ययोरिति । समासो नाम समसनं मिश्रणं एकीकरणं करणीतुल्यप्रमाणयोःसमासः । करण्युक्ता चतुरश्रस्याक्ष्णयारज्जुर्द्द्विस्तावतीं भूमिं करोति समस्येति । उक्तमनुभाषणं वक्ष्यमाणार्थं, इदमत्र परिशिष्यते, तादिदं वक्ष्यामीति ।

(नाना तदुक्तं)

नानाप्रमाणयोर्भिन्नप्रमाणयोःसमासः करण्युच्यते, ह्रसीयसः अल्पीयसश्चतुरश्चस्य करण्याकरणीप्रमाणेन, बर्षीयसःमहतश्चतुरश्रस्य, वृद्ध्रंचिह्नमेकदेशमुल्लिखेत्वृद्ध्रस्याक्ष्णयारज्जुरुभे नानाप्रमाणे चतुरश्रे समस्यति एकीकरोति । एतदुक्तं भवतिनानारप्रमाणे चतुरश्रे समस्य अल्पीयसश्चतुरश्रस्य करणीप्रमाणेन महदश्चतुरश्रस्य एकस्यां तिर्यङ्भान्यां परिच्छिन्द्यात् । तत आरभ्योर्ध्वां लेखां यथा परस्यां तिर्यङ्भान्यां तावति प्रदेशे निपतति तथा लिखेत् । लेखाविभक्तस्याल्पीयसः करणीप्रमाणं तिर्यङ्भानी । कस्य? महतः करणीप्रमाणपार्श्वमानीकस्य दीर्घचतुरश्रस्याक्ष्णयारज्जुरुमे नानाप्रमाणे चतुरश्रे समस्यति । चतुरश्र इति वर्तमाने पुनश्चतुरश्रग्रहणं मण्डलयोरपि चतुरश्रं कृत्वैव समासःसुकर इति ज्ञापयितुम् । तदुक्तंदीर्घस्येत्यादिना । अस्योपयोगो विद्याभ्यासादिषु ।

सुन्दरराजीया

(तुल्ययोःसमासः)

द्विकरण्या यथा द्विपुरुषेऽग्नौ पुरुषद्विकरण्या द्वयोः पुरुषयोःसमास इत्यादि । त्रिकरण्या त्रयाणां पुरुषाणां समासस्याप्येतदुपलक्षणं भवति ।

दीर्घचतुरश्रयोस्तु समासे अयं विशेषः । तिर्यङ्भान्या द्विकरणी तिर्यङ्भानी, पार्श्वमान्याश्च द्विकरणी पार्श्वमानीति । यथा द्विस्तावायामाश्वमेधवेद्यां षट्त्रिंशिकायाः पृष्ठ्याया द्विकरणी पृष्ठ्या । तिर्यङ्भान्योस्त्रिंशिकारान्तरेण वक्ष्यते । प्रक्रमस्य द्विकरणी प्रकमस्थानीया भवतीति । एवं दीर्घचतुरश्राणां समासे तिर्यङ्मान्यास्त्रिकरणी तिर्यङ्मानीति । पार्श्वमान्याश्च पार्श्वमानी । यथात्रिस्तावेऽग्नौ पक्षयोः पुरुषमात्रयाः तिर्यङ्मान्यास्त्रिकरणी अष्टाधिकशतद्वयाङ्गुला पञ्चतिलोना तिर्यङ्मानी भवति । पार्श्वमान्याश्च षडरत्नेः त्रिकरणी पञ्चाशह्द्विशताङ्गुला विंशतितिलोना पार्श्वमानी भवति । पुच्छस्य पार्श्वमान्या एकादशप्रादेशायाः त्रिकरणी अष्टाविंशतिद्विशताङ्गुला पार्श्वमानी । एवमन्यत्र ।

(नाना समासः)

उच्यत इति शेषः ॥

(हसीयसःतदुक्तं)

ह्रसीयसः करणीं तिर्यङ्मानीं कृत्वा वर्षीयसःसंबन्धिनं वृर्धं दीर्घचतुरश्रमुल्लिखेत्, वर्षीयसः करण्येव पार्श्वमानी । एवं कृतस्य दीर्घचतुरश्रस्याक्ष्णयारज्जुःसमस्तुयोः करणी भवति । तदुक्तं “दीर्घस्याक्ष्णयारज्जुः” इत्यादिना । यथा पञ्चविधेऽग्नौ क्लियमाणे द्विपुरुषेण चतुरश्रे कृते चतुष्पुरुषो भवति । तत्र पुरुषमात्रश्चतुरश्रः प्रक्षेप्तव्यः । तत्र द्विपुरुषकरणिके चतुरश्रे तदायामं पुरुषव्यासं दीर्घचतुरश्रमुल्लिखेत् । तस्याक्ष्णयारज्जुरष्टषष्टिशताङ्गुला सैकादशतिला, सा पञ्चविधाग्नेः करणी भवति ।

कपर्दिभाष्यम्

चतुरश्राच्चतुरश्रं निर्जिहीर्षन् यावन्निर्जिहीर्षेत्तस्य करण्या वर्षीयसो वृद्ध्रमुल्लिखेत् ॥ २.५ ॥

If it is desired to remove a square from another, a (rectangular) part is cut off from the larger (square) with the side of the smaller one to be removed;

चतुरश्राच्चतुरश्रं निर्जिहीर्षन् यावन्निर्जिहीर्षेत्तस्य करण्या वर्षीयसो वृद्ध्रमुल्लिखेत् ॥ २.५ ॥

पूर्वस्माच्चतुरश्राच्चतुरश्रं निर्जिहीर्षन् चतुरश्रप्रमाणेन वृध्रमुल्लिखेत् ।

वृर्धस्य पार्श्वमानीमक्ष्णयेतरत्पार्श्वमुपसंहरेत् ॥ २.५ ॥

the (longer) side of the cut-off (rectangular) part is placed across so as to touch the opposite side;

वृर्धस्य पार्श्वमानीमक्ष्णयेतरत्पार्श्वमुपसंहरेत् ॥ २.५ ॥

संयोजयेत् ।

सा यत्र निपतेत्तदपच्छिन्द्यात् ॥ २.५ ॥

by this contact (the side) is cut off.

सा यत्र निपतेत्तदपच्छिन्द्यात् ॥ २.५ ॥

सा पार्श्वमानी इतरस्मिन् पार्श्व यत्र निपतति स्पृशति तत्रापच्छिन्द्यात् ।

छिन्नया निरस्तम् ॥ २.५ ॥

With the cut-off (part) the difference (of the two squares) is obtained.

छिन्नया निरस्तम् ॥ २.५ ॥

छिन्नया निरस्तीकृते तन्निरस्तं भवति ।

करविन्दीया व्याख्या

(चतुरश्रातछिन्नया निरस्तम्)

चतुरश्रादिति । इदमपि करणीविधानमेव । महतश्चतुरश्रादल्पं चतुरश्रं निर्जिहीर्षन् विहर्तुमिच्छन् यावत्प्रमाणं चतुरश्रमपनेतुमिच्छति तस्याल्पस्य सरण्या माहतश्चतुरश्रस्यैकदेशं यथा छिन्नं भवति तथोल्लिखेत् । एवं कृते छिन्नं निरसि तव्यक्षेत्रप्रमाणतिर्यङ्भानीकं महत्क्षेत्रपार्श्वमानीकं प्रमाणपार्श्व मानीकं दीर्घचतुरश्रं भवति । अस्य क्षेत्रस्य पार्श्वमानीमक्ष्णयेतरत्पार्श्वमुपसंहरेत्गमयेत्, सा पार्श्वमानीमक्ष्णयेतरता यत्रेतरस्याः पार्श्वमान्याः प्रदेशे निपतति तदपछिन्द्यात्पार्श्वमानीमपाच्छित्याधिकं त्यजेत्, छिन्नया निरस्तंछिन्नं पार्श्वमानीनिरसितव्यक्षेत्रस्य करणी भवति । तया पार्श्वमान्या चतुरश्रे कृते निरसितव्यक्षेत्रं निरस्तं भवतीत्यर्थः ।

सुन्दरराजीया व्याख्या

चतुरश्रातछिन्नया निरस्तम्

निर्हारोनिरसनम् । यथा निविधेऽग्नौ क्रियमाणे द्विपुरुषेण चतुरश्रे कृते चतुष्पुरुषो भवति । तत्रैकपुरुषत्यागार्थं पुरुषमात्रतिर्यङ्भान्या वृध्रमुल्लिख्य तस्योत्तरां पार्श्वमानीं दक्षिणां प्राचीमितरत्पार्श्वं गमयेत् । सा च तत्र द्विपुरुषप्रमाणायां चत्वारिंशच्छतद्वयाङ्गुलप्रमाणायां पञ्चतिलाश्वापच्छिन्द्यात् । परिशि ष्टया करण्या चतुरश्रे कृते पुरुषो निरस्तो भवति ।

कपर्दिभाष्यम्

यथा स्वयमेव दर्शयति

उपसंहृताक्षणयारज्जुः सा चतुष्करणी छिन्ना चेतरा च यत्पृथग्भूते कुरुतस्तदुभयं करोति ॥ २.६ ॥

That (the longer side of the cut-off rectangle in the above rule) which is placed across is the diagonal equal to the side of a square four times as large (as the given square). The area (of the squares) produced separately by the cut-off side and the other (the breadth of the rectangle) together equal the the area (of the square) produced by this diagonal.

उपसंहृताक्षणयारज्जुः सा चतुष्करणी छिन्ना चेतरा च यत्पृथग्भूते कुरुतस्तदुभयं करोति ॥ २.६ ॥

उपसंहृता पूर्वं पार्श्वमानी । इदानीमक्ष्णयारज्जुश्च रश्रस्यसा चतुष्करणी द्विपुरुषात्छिन्ना पार्श्वमानी इतरातिर्यह्भानी यत्पृथग्भूते कुरुतः तदुभयं करोति ॥

कथमित्याह

तिर्यङ्मानी पुरुषं शेषस्त्रीन् ॥ २.६ ॥

If the breadth produces one square purușa, the other side produces three square purușas.

तिर्यङ्मानी पुरुषं शेषस्त्रीन् ॥ २.६ ॥

तिर्यङ्भानी पुरुषं करोति । शेषस्त्वक्ष्णयारज्जुद्वौ । तदुभयं तस्याक्ष्णयारजुरिति त्रीन्करोति ॥

तदुक्तम् ॥ २.६ ॥

This has been stated.

2.4-2.6. Āpastamba’s methods for making a square out of a combination or differ- ence of two squares are exactly the same as those of Baudhāyana, discussed in B§l. 2.1-2.2. The sūtra Āśl. 2.6 is an application of the combination of two squares, for instance $a^2+3a^{2}4a^2$, where a is the measure or producer of the square.

तदुक्तम् ॥ २.६ ॥

तच्चाप्युक्तम् ॥

करविन्दीया व्याख्या

इमं प्रकारमुदाहरणमुखेन स्पष्टिकरिष्यन्नाह

उरसंहता तदुक्तमुपेति । सर्वतो द्विपुरुषप्रमाणं चतुष्पुरुषं चतुरश्रं विषयीकृ त्योदाहरति । एकस्य चतुरश्रस्यावयवभूते दीर्घचतुरश्रे या पार्श्वमान्यक्ष्णयोपसंहृता सा चतुष्करणी चतुष्करणी चतुष्पुरुषकरणीति प्रतिज्ञाता । अस्य तिर्यङ्भानी च पुरुषमात्रकरणीति । अस्य दीर्घचतुरश्रस्य छिन्ना पार्श्वमानी कियत्करणीति न ज्ञाता, सैवात्रावगन्तव्या । अत्र पुरुषप्रमाणं तिर्यङ्भान्या पृथग्भूतया यत्क्रियते छिन्नया पार्श्वमान्या पृथग्भूतया यत्क्रियते अक्ष्णयारज्जुः तदुभयक्षेत्रकरणीति न्यायतोऽवगता । तत्राक्ष्णयारज्जुफलभूताच्चतुष्पुरुषाच्चतुरश्रादेकप्रमाणं तिर्यङ्भानीफले त्वेकस्मिन्नपनीते त्रयः पुरुषाः परिशेष्यात्सा त्रिपुरुषकरणीत्यवगन्तव्या । अत इदमुक्तं तिर्यङ्भानी पुरुषं करोति शेषः छिन्ना पार्श्वमानी । त्रीन् पुरुषानिति पुल्लिङ्गनिर्देशः पुरुषभिप्रायः । पुरुषनिर्देशश्वाग्नौ पुरुषेण विमानं पुरुषाभ्यासापचयौ समासनिर्हारयोः उदाहरणमिति । अयमर्थःसर्वतो द्विप्रमाणाच्चतुष्पुरुषाच्चतुरश्रादेकं पुरुषमपनीय त्रिपुरुषं समचतुरश्रं कर्तुमिच्छन् तच्चतुरश्रं पुरुषप्रमाणया रज्ज्वा मध्ये परिच्छिद्य द्विधा कृत्वा तदर्घस्यैकां पार्श्वमानीमपरां पार्श्वमानीं प्रत्यक्ष्णयोपगमयित्वा तयोर्यत्र संपातः तत्रावस्थितां पार्श्वमानीं छिच्वावशिष्टं निरस्य शिष्टया पार्श्वमान्या समचतुरश्रे कृते तच्चतुरश्रं त्रिपुरुषचतुरश्रं भवति । तथा सर्वतश्वतुष्पुरुषाच्चतुरश्राच्चतुरः पुरुषानपनीय द्वादशपुरुषं समचतुरश्रं कर्तुमिच्छद्द्विपुरुषप्रमाणया तिर्यङ्भान्या समचतुरश्रं विभज्यार्धस्यैकां पार्श्वमानीमन्यां प्रति गमयित्वा तयोःसन्निपातेऽवस्थितां पार्श्वमानीमवच्छिद्य छेदं निरस्य शिष्टया पार्श्वमान्या चतुरश्रे कृते तत्क्षेत्रं द्वादशपुरुषसमचतुरश्रं भवति । छिन्नशिष्टा पार्श्वमानी तत्करणी भवतीत्यर्थः । एवं प्रमाणक्षेत्रे तृतीयद्विकरणीमपनीय तृतीयकरणी भवति । एवमेव सर्वत्र चतुष्करणीचतुर्थकरणीप्रभृतयः करण्योऽवगन्तव्याः । तदुक्तं “दीर्घस्याक्ष्मयारज्जुरित्यनेन । अस्योपयोगो द्रोणादिषु, सुन्दरराजीया व्याख्या

तदेवोदाहरति

उपसंहृता तदुक्तम्

या अक्ष्णयोपसंहृताएकीभूता रज्जुःसा चतुष्करणी द्विपुरुषापच्छिन्ना पार्श्वमानी अपच्छिन्ना पञ्चतिलोनाष्टशतद्वयाङ्गुला । इतरापुरुषमात्री तिर्यङ्भानी च यत्पृथग्भूते कुरुतस्तदुभयं करति कर्णरज्जुत्वात् । तत्र तिर्यङ्भानी स्पष्टमेव हि पुरुषमात्रं करोति । पारिशेष्यात्पार्श्वमानी त्रीन् पुरुषान् करोतीति ज्ञातुं शक्यते । तदुक्तं “दीर्घस्याक्ष्णयारज्जुः” इत्यादिना ।

कपर्दिभाष्यम्

दीर्घचतुरश्रं समचतुरश्रं चिकीर्षन् तिर्यङ्मान्यापच्छिद्य शेषं विभज्योभयत उपदध्यात् ॥ २.७ ॥

If it is desired to transform a rectangle into a square, a (square) part is cut off (from the rectangle) by the breadth. The remainder (of the rectangle) is divided (into two equal parts) and placed on two sides.

दीर्घचतुरश्रं समचतुरश्रं चिकीर्षन् तिर्यङ्मान्यापच्छिद्य शेषं विभज्योभयत उपदध्यात् ॥ २.७ ॥

दीर्घचतुरश्रं समचतुरश्रं कर्तुमिच्छन् तिर्यङ्भन्या तिर्यङ्भानीप्रमाणेनापच्छिद्य शेषं विभज्यद्विधा कृत्वा तदुभयतः अग्रतः पार्श्वतश्रोपदध्यात्निक्षिपेत् ।

खण्डमागन्तुना संपुरयेत् ॥ २.७ ॥

The empty space (in the corner) is filled up with a (square) piece.

खण्डमागन्तुना संपुरयेत् ॥ २.७ ॥

खण्डमागन्तुनातिरिक्तेन पूरयेत् । पूरयित्वा तदतिरिक्तं त्यचेत् ।

तस्य निर्हार उक्तः ॥ २.७ ॥

The removal of it (of the square piece from the square thus formed to get the required square) has been stated.

2.7. The same method of transformation of a rectangle into a square as given by Baudhāyana in his Bŝl. 2.5 is discussed.

तस्य निर्हार उक्तः ॥ २.७ ॥

तस्य त्यागविधिरुक्तः ।

इति द्वितीयः खण्डः

करविन्दीया व्याख्या

दीर्घचतुरश्रंनिर्ह्रास उक्तः

दीर्घोतिसर्वतस्तुल्यप्रमाणं समचतुरश्रं एकत आयामतोऽधिकं दीर्घचतुरश्रं समचतुरश्रं कुर्वन् तिर्यङ्भान्या तिर्यङ्भानीप्रमाणया रज्ज्वा परिमिते प्रदेशे मध्ये दक्षिणोत्तरमप च्छिद्य शेषं पुर्वभागं मध्ये दिर्यक्द्विधा विभज्य तयोः पश्चिमं भागं तथैवावस्थाप्य पूर्वभागं प्रथमस्योत्तरतः प्राचीनमुपदध्यात् । उत्तरपूर्वभागं शून्यभूतं खण्डमागन्तुना संपूर्य समचतुरश्रं संपाद्य अधिकमागन्तुभूतं खण्डं ततो निर्हरेत्निर्गमयेत् । तस्य निर्हार उक्तः “चतुरश्राच्चतुरश्रं निर्झिहीर्षन्” इति । तस्योपयोगो रथचक्त्रादिषु ।

इति द्वितीयः खण्डः

सुन्दरराजीया व्याख्या

दीर्घचतुरश्रंनिर्हार उक्तः

तिर्यङ्भानीप्रमाणेन पार्श्वमानीमपच्छिद्य समचतुरश्रं कृत्वा शेषं विभज्य पुरस्तादुत्तरतश्वोपदधयात्, यथोत्तरपूर्वकोणे समचतुरश्रं आगन्तुः खण्डो भविष्यति । तस्य निर्हार उक्तः “चतुरश्राच्चतुरश्रम्” इति ॥

इति द्वितीयः खण्डः

कपर्दिभाष्यम्