१९

श्मशानचितं चिन्वीतेति विज्ञायते १

According to tradition, a fire-altar in the form of a pyre (śmaśānacit) is to be constructed.

श्मशानचितं चिन्वीतेति विज्ञायते १

सर्वमग्निं चतुरश्रान्पञ्चदश भागा-न्कृत्वा तेषामाख्यातमुपधानम् २

The entire (area of the) fire-altar is divided into 15 square-parts. How to do this has been stated.

THE CONSTRUCTION OF FIRE-ALTARS IN THE FORM OF A PYRE (ŚMAŚĀNACIT).

19.1-19.2. The fire-altar in the form of a pyre, as we shall presently see, is a trapezium. For its measurements and constructions as also for the bricks, a new unit has been introduced. Let p be this unit. According to rule 19.2,

\(p^2 =\frac{1}{15}\) of the area of the fire-altar \(= \frac{1}{15}\times \frac{15}{2} sq. pu.

\(= \frac{1}{2}\) sq. pu.

\(p = \frac{1}{\sqrt{2}} pu. = \sqrt{7200} aṅg. 84 aṅg. 28 tila.\)

Dvārakānātha explains: agnikṣetram…pañcadaśadhā vibhajya labdhaṁ saptasahasrāņi dve śate cāñgulayaḥ | tasya bhāgasya samacaturaśrakaraṇī ṣaṭtilonapañcāśītyaṅgulā (85 aṁg. -6 ti.).

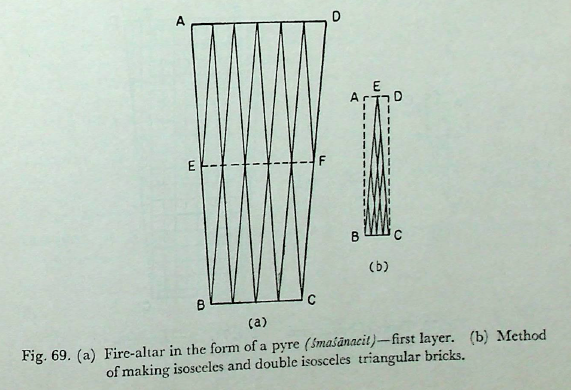
Fig. 69. (a) Fire-altar in the form of a pyre (śmaśānacit)—first layer. (b) Method of making isosceles and double isosceles triangular bricks.

The fire-altar is in the form of a trapezium ABCD, of which the western side BC is 2p units (= 170 aṅg. 12 tila), the eastern side AD is 3p ( 254 aṅg. + 16 tila) and the height, that is, the distance between AD and BC is 6p (509 aṅg. - 2 tila) (Fig. 69). For the word trapezium, the word ekato’nimaddirghacaturaśra is used. It means a rectangle of which one side is shorter (than the opposite parallel side). The area of the trapezium is given by

\(2p \times 6p + \frac{p}{2} \times 6p = 15p^2 = \frac{15}{2}sq. pu. = 7\frac{1}{2} sq. pu\)

which satisfies the area of the agnikṣetra.

First layer. For purposes of making the bricks, a rectangle ABCD is formed such that its length AB is 3p and breadth BC is \(\frac{1}{2}p\). From the mid-point E of AD, join EB, EC. EBC is an isosceles triangle (prauga) of area \(\frac{3}{4}p^2\). 20 such praugas equal 15p^2 or \(7\frac{1}{2}\) sq. pu. and can be accommodated within the fire-altar. To attain the number 200, each such isosceles triangle is divided into 10 parts in the manner shown in Fig. 69(b). The sides EB, EC and BC are each divided into 4 equal parts by marking 3 equidistant points on each side. The points on the sides are joined with those on the base as shown, so as to obtain 4 isosceles triangles at the base and 6 double isosceles triangles above them. About the formation of such triangles, the commentator says: evam vibhakte pṛthvanikasthāḥ praugākārāścatasra iṣṭakāḥ | tatastisra ubhayataḥ praugākṛtayaḥ | tato dve | tata ekā cubukāntā |

Regarding the placement of 20 isosceles triangles EBC of area \(\frac{3}{4}p^2\), a line EF is drawn in the middle of the body (Fig. 69a). In the eastern half, 11 such triangles can be placed, 6 with vertices turned west and 5 with vertices turned east. In the western half, 9 such triangles can be accommodated, 5 with vertices turned west and 4 with vertices turned east. This represents the arrangement of bricks in which 80 praugas and 120 ubhayata praugas are used.

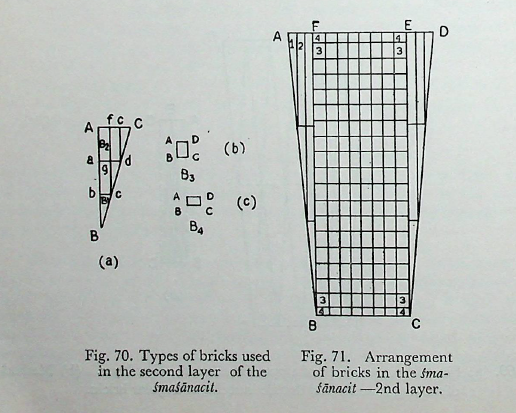
Fig. 70. Types of bricks used in the second layer of the śmaśānacit.

Fig. 71. Arrangement of bricks in the śmaśānacit-2nd layer.

सर्वमग्निं चतुरश्रान्पञ्चदश भागा-न्कृत्वा तेषामाख्यातमुपधानम् २

त्रिभिर्भागैर्भागार्धव्यासं दीर्घचतुरश्रं विहृत्य पूर्वस्याः करण्या मध्याच्छ्रोणी प्रत्यालिख्यान्तावुद्धरेत् । तस्य दशधा विभागः ३

A rectangle is made with its length equal to thrice (the side of) the square- part and breadth equal to half (the side of the square-part). Lines are drawn from the middle of its eastern side to the two western corners and the two outer parts are removed (so as to obtain an isosceles triangle). This (isosceles triangle) is divided into 10 parts.

त्रिभिर्भागैर्भागार्धव्यासं दीर्घचतुरश्रं विहृत्य पूर्वस्याः करण्या मध्याच्छ्रोणी प्रत्यालिख्यान्तावुद्धरेत् । तस्य दशधा विभागः ३

तानि विंशतिः सर्वोऽग्निः सम्पद्यते ४

The entire fire-altar is composed of 20 of them (of such isosceles triangles).

तानि विंशतिः सर्वोऽग्निः सम्पद्यते ४

अपरस्मि-न्प्रस्तारे प्रौगमध्येऽनूचीनं विभजेत् । तस्य षड्धा विभागः । ते द्वे पर्श्वयोरुपदध्यात् ५

In the other layer, one of the (five) isosceles triangles (into which the entire fire-altar can be divided) is to be vertically bisected. Each half is divided into 6 parts. These two (half isosceles triangles each divided into 6 parts) are to be placed on either side (the southern and the northern side of the fire-altar).

अपरस्मि-न्प्रस्तारे प्रौगमध्येऽनूचीनं विभजेत् । तस्य षड्धा विभागः । ते द्वे पर्श्वयोरुपदध्यात् ५

भागतृतीयायामश्चतुर्थव्यासाः कारयेत् । तासाम-र्ध्यास्तिर्यग्भेदाः ६

Bricks of length equal to one-third (the side of the square part) and breadth equal to one-fourth (the side of the square part) are to be made, and then half of such bricks by transverse bisection.

भागतृतीयायामश्चतुर्थव्यासाः कारयेत् । तासाम-र्ध्यास्तिर्यग्भेदाः ६

ता अन्तयोरुपधाय शेषमग्निं बृहतीभिः प्राचीभिः प्रच्छादयेत् । अर्धेष्टकाभिः सङ्ख्यां पूरयेत् ७

After placing them (the half bricks) on the two ends (the eastern and the western), the rest of the fire-altar is to be covered with the bṛhatī bricks turned towards east, and the number (of 200 bricks) is to be completed with half bricks.

19.5-19.7. Bricks and their placement in the second layer. The entire space of the fire-altar (agnikṣetra) can be divided into five large isosceles triangles of base p and height (from vertex to base) 6p. Three of them have their vertices turned towards west and the vertices of the two in between them are turned towards east. The two isosceles triangles, one on the southern side and the other on the northern, which have their vertices turned towards west, are bisected by perpendicular lines drawn from the vertex to the base (Fig. 71). The agnikṣetra is thus divided into three portions, (1) half isosceles triangle CDE on the southern side, (2) the half isosceles triangle BAF on the northern side, and (3) the rectangle BCEF in the middle. Note that, since ED and AF are each \(\frac{1}{2}p\), EF = BC = 2p.

To make the different types of bricks, the half isosceles triangle on either side is divided into six parts (Fig. 70). AB, BC and AC are divided into three equal parts each by the points, a, b, c, d, e, and f. Join bc, ad, de and cgf. The space is thus divided into 3 half isosceles triangles Bbc, cdg and dce which constitute the first type of brick B1. Note that \(Bb = 2p, bc = \frac{p}{6}.\) Through the above division, we get the second type B2, the rectangular bricks abcg, Aagƒ and fgde, of which the sides are 2p and p . The third type B, called the bṛhati, is a rectangular brick ABCD (Fig. 70(b)), of which AB = 1\3p and AD =1/4p. The fourth type \(B_{4}\) is half bṛhati (Fig. 70(c)), a rectangular brick measuring p/4 by p/6.

The arrangement of bricks in the second layer is shown in Fig. 71. 3B1s and 3 B2s are placed in each of the two half-isosceles parts of the fire-altar. 8 B1s are placed on the eastern and the western parts each of the rectangular part of the fire- altar, with the longer side turned north-south. (Note that \(2p/\frac{1}{4}p = 8\)). These two rows use up up and the remaining vertical distance is (\(6p—\frac{p}{3} = \frac{17p}{3}.\)) The remaining space in the rectangular part of the fire-altar can be divided into 17 horizontal and 8 vertical rows in which 136 B3 bricks can be fitted with their longer sides turned east. Thus, the number of bricks used in this way totals as follows :

\(B_{1} — 6; B_{2} — 6 ; B_{з} — 136; B_{4} - 16; total — 164.\)

There is still a deficit of 36 bricks. According to the commentator, the deficit can be met by replacing 36 B3 bricks (9 from each of the 4 corners) by 72 B4s. Dvārakā- nātha says: pārśvayorupahitapraugārdhayordvādaśeṣṭakāḥ | madhyabhūtacaturaśra (pūrvā) parāntayoḥ ṣoḍaśārdheṣṭakāḥ | madhye şaṭtrimsacchalam bṛhatyaḥ prāgāyatāḥ | evam catuḥṣaṣṭi satamiṣṭakaḥ ṣaṭtrimśannyūnā bhavanti | śronyamseṣu nava nava bṛhatiścaturasrakṛtā uddhṛtyāṣṭādaśāṣṭāḍaśārdhyā nidheyāḥ | evam dviśataḥ prastārāḥ |

ता अन्तयोरुपधाय शेषमग्निं बृहतीभिः प्राचीभिः प्रच्छादयेत् । अर्धेष्टकाभिः सङ्ख्यां पूरयेत् ७

ऊर्ध्वप्रमाणमग्नेः पञ्चमेन वर्धयेत् ८

The height of the fire-altar is to be increased by one-fifth (of the jānu, that is, \(6\frac{2}{3}\) angula).

ऊर्ध्वप्रमाणमग्नेः पञ्चमेन वर्धयेत् ८

तत्सर्वं त्रेधा विभज्य द्वयोर्भागयोश्चतुर्थेन वा नवमेन वा चतुर्दशेन वेष्टकाः कारयेत् ९

The whole of it (the height including the added 5th part) is divided into three parts and bricks are made with the fourth or the ninth or the four- teenth part of the two of these three parts (according as the fire-altar is intended to have 5, 10 or 15 layers).

तत्सर्वं त्रेधा विभज्य द्वयोर्भागयोश्चतुर्थेन वा नवमेन वा चतुर्दशेन वेष्टकाः कारयेत् ९

ताभिश्चतस्रो वा नव वा चतुर्दश वा चितिरुपधाय शेषमवाञ्चमक्ष्णयापच्छिन्द्यात् । अर्धमुद्धरेत् १०

With these bricks, 4 or 9 or 14 layers are made, the remaining layer (of thickness equal to one-third of the height) is diagonally cut in the downward direction and half of it removed.

ताभिश्चतस्रो वा नव वा चतुर्दश वा चितिरुपधाय शेषमवाञ्चमक्ष्णयापच्छिन्द्यात् । अर्धमुद्धरेत् १०

तस्य नित्यो विभागो यथायोगमिष्टकानां ह्रासवृद्धि ११

Its division is exact. Larger and smaller bricks are taken according as these fit.

19.9-19.11. These sūtras deal with the height of the fire-altars and do not call for much comment.

तस्य नित्यो विभागो यथायोगमिष्टकानां ह्रासवृद्धि ११